Tipiskos ieteikumus risinājuma meklēšanai var iedalīt divās grupās: 1) jāmācās cītīgāk, lai iegaumētu, jāvingrinās vairāk, vairāk jāuzdod mājas darbu utt., 2) jāmazina vai jāatvieglo saturs, jo šīs paaudzes bērni nevar to un to. Pirmo ieteikumu grupu raksturo kāda jau esoša rīka izcelšana un pārspīlēšana, bet gan prakse, gan pasaules vadošie metodikas pētnieki parāda, ka mainīgajā pasaulē arī skolai, tostarp mācīšanas un mācīšanās veidam, ir jāmainās. Savukārt otrā ieteikumu grupa ir praksē pārbaudīta, un tās tālāka neapdomīga īstenošana ir bīstama no valsts pasūtījuma skatpunkta – matemātikas specifiskais saturs Latvijā ir samazināts vairākkārt, bet tas negūst izpausmi dziļākās zināšanās, drīzāk otrādi, ko apliecina tas, ka nosacīts vidējais rezultāts skaitliski paliek tajā pašā līmenī.

Kur meklējams risinājums? Kopā ar kolēģiem, strādājot pie pilnveidotā matemātikas satura, šo risinājumu redzējām dziļākas izpratnes veidošanā skolēniem par matemātikas jēdzieniem, darbībām un paņēmieniem. Skaidri nošķīrām apzīmējumus dziļāka izpratne un sarežģītāks saturs. Saturs netika mehāniski papildināts, tika plānotas noteiktas mācību darbības izpratnes/jēgas veidošanai. Kādu mācību darbību rezultātā varam sagaidīt dziļāku izpratni? Patiesas izpratnes veidošana iet roku rokā ar kritiskās domāšanas un problēmrisināšanas prasmju veidošanu un tālāku pilnveidi. Lai fokusētu domu, izmantošu 1. klases saturu. Skolēns jēdzienu vai darbību izdzīvo praktiskā darbībā, attēlošanai izmanto dažādus modeļus, dotas un paša veidotas vizualizācijas, skaidro vārdiski savu darbību, saskata un skaidro matemātisku objektu un darbību īpašības, mēģina tās pamatot; lūko skaidrot, kāpēc tieši tā rīkojās, uzklausa un apspriež citu veidotos risinājumus, meklē dažādus risinājumus, izvērtē kļūdas un saskata dažādas iespējas to labošanai, izvēlas sev piemērotu paņēmienu darbības veikšanai un paskaidro tā izvēli, veido savai domu gaitai atbilstošu pieraksta veidu u. tml. Jebkuru pārmaiņu ieviešanā ir riski, ka to īstenojumā dažas idejas tiks pārspīlētas vai uztvertas formāli. Vai katram 1. klases skolēnam divu skaitļu saskaitīšanai jālieto visi iespējamie paņēmieni? Noteikti nē! Pieeja pēc būtības vēlama tāda, ka skolēns, kurš 8 + 7 redz kā 8 + 2 + 5, tā arī domā un raksta; tas, kurš šo darbību redz kā 5 + 3 + 7, saņem atbalstu tā domāt un rakstīt arī turpmāk; tas, kurš ir iegaumējis vienādu skaitļu summas, saņem atbalstu to izmantot arī šeit un rakstīt 1 + 7 + 7; tas, kuram lielākais atbalsts skaitļa sastāva modelēšanai līdz šim ir bijusi tabula 2*5, varbūt izvēlēsies domāšanas gaitu 5 + 3 + 5 + 2. Paņēmienu dažādību nosaka konkrētās klases skolēnu pieredze, veids, kā viņi ir tendēti domāt. Ja pēc kāda no paņēmieniem nav “pieprasījuma”, tad ir prātīgi to tikai pārrunāt.

Vai skolēni ir gatavi domāt, vai 1. klases skolēnam patīk domāt, vai intelektuāls izaicinājums savam prātam matemātikā ir tikpat dabisks un nozīmīgs, kā izaicinājums savam ķermenim sporta nodarbībā? Ne jau tāpēc matemātika sagādā grūtības, ka “daudz jādomā”. Nav pamata vispārinājumam, ka skolēniem nepatīk domāt un tāpēc arī matemātika nepatīk. Viens no šo grūtību un nepatikas patiesajiem cēloņiem slēpjas tajā, ka skolēniem ir neskaidrs domāšanas statuss matemātikā. Kāpēc mans pareizais risinājums tika atzīts par nepareizu vai nepieļaujamu? Kāpēc es tā nevarēju rīkoties? Kā tad drīkst domāt? Kā ir pareizi domāt matemātikas stundās? Citiem vārdiem sakot – skolēniem, kādam agrāk, kādam vēlāk, pazūd saikne starp iedzimto, pieredzē sakņoto spriestspēju un “domāšanu matemātikā”. Intereses un motivācijas zudums ir objektīvas sekas. Jo īpaši sākumskolas skolotājiem svarīgi šo saistību apzināties; uzturēt, atbalstīt un izmantot skolēnu neformālo, pieredzē balstīto spriešanu līdztekus matemātikai raksturīgajām deduktīvās spriešanas formām. Tas nenozīmē to, ka nav jālabo patiešām aplami risinājumi un spriedumi. Svarīgi ir pārprasta zinātniskuma vārdā “nenokaut” bērnu gatavību izmantot loģiku, spriest no konkrētā uz vispārīgo. Ilustrācijai izmantošu 3./4. klasei atbilstošu uzdevumu: Divās mucās kopā ir 55 laši. Vai vienā mucā var būt par 10 lašiem vairāk nekā otrā mucā? Ja skolēns var paskaidrot katrā solī veikto, tad nekādā ziņā nav peļams tipiski gaidītais un zinātniski korektais risinājums: 55 – 10 = 45, 45 ar 2 nedalās, tā nevar būt. Vienlaikus ir svarīgi, ka tiek pieņemts risinājums, kura pamatā ir gadījumu pārlase: ... 31 un 21; 32 un 22; 33 un 23; ... es ņēmu visus variantus pēc kārtas un secinu, ka tā nevar būt. Šādi spriest naturālo skaitļu kopā ir matemātiski korekti.

Pakāpeniski matemātikas mācīšanos veidosim kā izpētes procesu, kura subjekti ir konkrētā bērnu grupa. Droši vien arī turpmāk atsevišķos gadījumos mācīšanos būs piemēroti uzsākt ar: es jums pastāstīšu par to un to, vai šodien mācīsimies par to un to, bet tiecība ir uz tādu matemātikas mācīšanās procesu, kura katrs posms sākas ar skaidri formulētu mācīšanās mērķi kā jautājumu, kas ierosina domāšanu, kāpēc ..., ko nozīmē ..., kā var rīkoties ... u. tml., dodot iespēju bērniem izteikt pirmās idejas. Ir saprotamas skolotāju bažas, jo plānotais process var aiziet citu gaitu, var uzrasties arī iepriekš neparedzēti jautājumi un situācijas, bet svarīgi, ka skolotājs nebaidās kopā ar skolēniem meklēt risinājumus neviennozīmīgās situācijās, reizēm tā nonākot pie kādas autentiskas problēmas. Ir vēl viens iemesls, kāpēc tik svarīgi izcelt jautājumu kā izteikuma veidu. Ja skolēnam nav pieredzes dzirdēt skolotājas formulētos jautājumus, atbildes uz tiem, ja viņam trūkst pieredzes pašam skaļi formulēt jautājumus, iegūt atbildes, formulēt nākamos jautājumus, tad nav pamata cerēt, ka “notiks domāšana” kā strukturēta iekšējā runa: jautājums, atbilde, jautājums, atbilde, jautājums, ...

Viens no tradīcijā tipiskiem sašaurinājumiem domāšanas kontekstā matemātikā ir fokusēšanās uz gala rezultātu, t. sk., analizējot kļūdas risinājumā. No kritiskās domāšanas prasmju skatpunkta ir vērtīgi, ja skolēni domā par vairākiem iespējamiem kļūdu cēloņiem, piemēram, analizējot un labojot vienādību 3 + 5 = 7, viņi raksta ne tikai tipisko 3 + 5 = 8, bet arī 2 + 5 = 7, 3 + 4 = 7, 3 + 5 > 7.

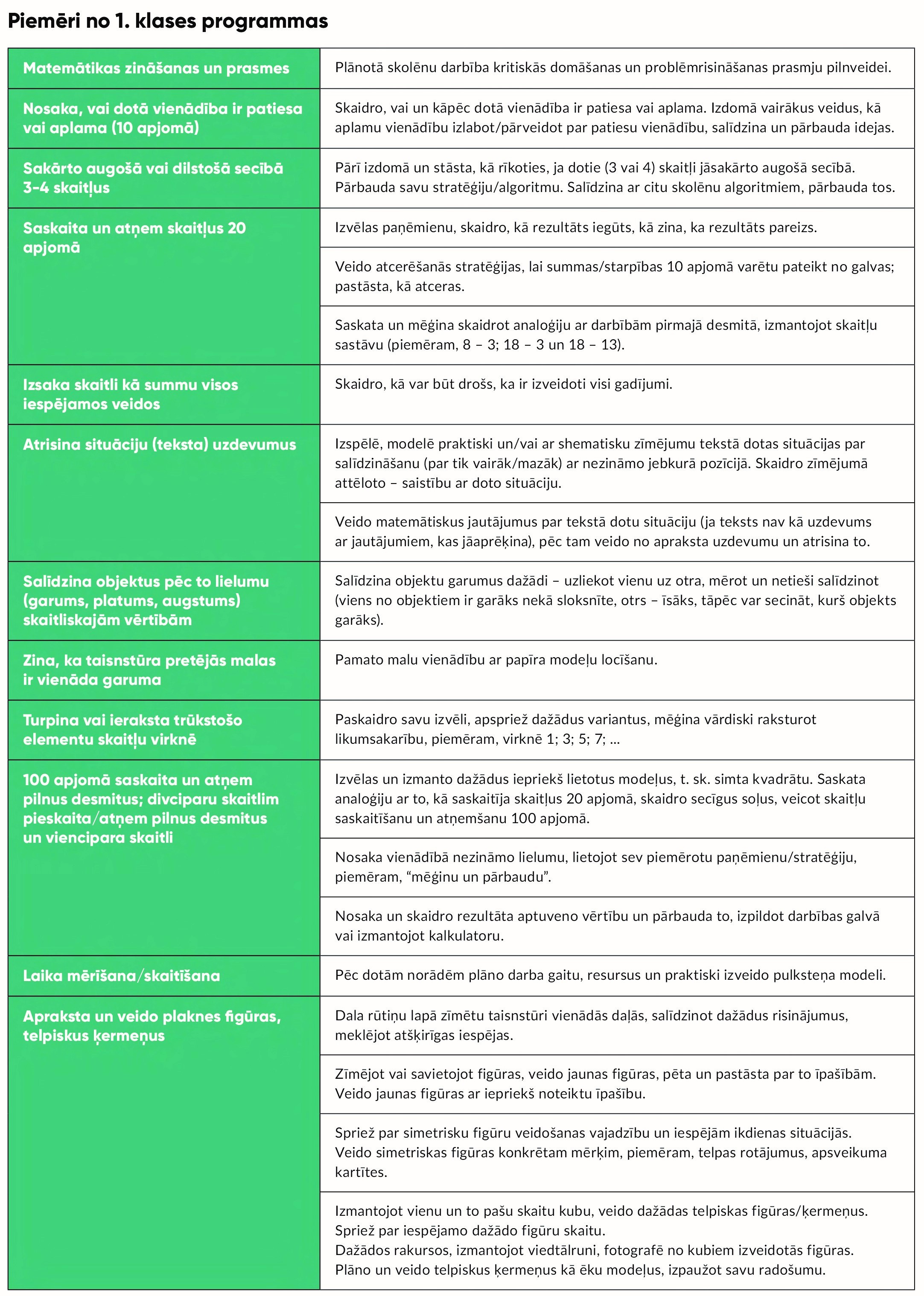
Pilnveidotās programmas veidotāji ir cieši pārliecināti, ka skolēni var daudz vairāk, nekā tradīcijā tiek uzskatīts, jo īpaši tas attiecināms uz domāšanu. Šī pārliecība transformējas ļoti konkrētos un vecumam atbilstošos skolēnu darbību aprakstos (sk. piemērus tabulā). Apkopojoši šo pieeju varētu raksturot šādi: skolēna patstāvīga spriešana (skolotāja mērķtiecīgi vadīta) ir īpaši veicināma atklāšanas, sākotnējās izpratnes veidošanas fāzē un jau apgūtā, vingrināšanās rezultātā nostiprinātā satura dziļākas izpētes fāzē, risinot uzdevumus, kas liek meklēt risinājumu nepazīstamās situācijās.