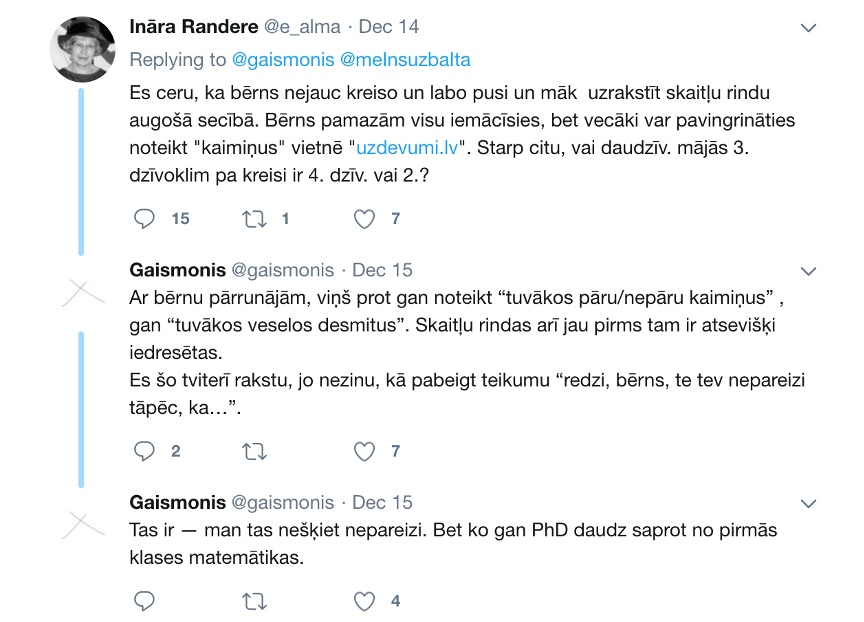
Vairākas pareizās atbildes. Arī matemātikā.

Publicētais labotais skolēna darbs matemātikā, Twitter, 13. decembris
Skolēnam, risinot uzdevumu, ir personiska pieredze un mācīšanās laikā veidotā izpratne
Pirmkārt, ir jāpieņem, ka ikvienam skolēnam ir gan personiskā pieredze, gan mācīšanās rezultātā iegūtā izpratne. Pieredze skolēnam saka, ka secīgus skaitļus var pierakstīt divējādi. Piemēram, sienas kalendārā blakusesošie skaitļi arvien pieaug, bet uz tēva automašīnas numura zīmes arvien samazinās.
Mācīšanās procesā izpratni par to, kas ir “skaitļa kaimiņi”, var veidot dažādi. Šī jēdziena ieviešanā var izmantot skaitļu ass attēlojumu vai izpratni par to, ko nozīmē “par 1 lielāks / mazāks”. Vēl labāk, ja izmantotas abas pieejas. Ja skaitļu ass koncepts skolēniem vēl nav zināms, tad drīzāk nav pamata gaidīt izkārtojumu tikai pieaugošā secībā.
Vērtēšanas mērķis
Uzdevums ir piemērots, lai novērtētu, vai skolēns saprot, kas ir skaitļa “kaimiņi”, un var tos uzrakstīt. Mēs nezinām, ar kādu mērķi skolotāja šo uzdevumu deva skolēniem. Risinājums novērtēts kā aplams, lai gan uzdevuma formulējums neprasa noteiktu secību. Skolēns uzdevumu ir atrisinājis pilnīgi pareizi. Ja skolotājas mērķis bija noskaidrot, vai skolēni var uzrakstīt skaitļus pieaugošā secībā, tad bija jāizvēlas cits uzdevums.
Ja izvērtējot bija šaubas par to, vai konkrētais skolēns var uzrakstīt augošā secībā, sākot ar mazāko, tad to varēja pajautāt nākamajā stundā, un tas būtu pamats, lai izliktu galīgo vērtējumu.
Vērtēšanas kritēriji
Konkrētais piemērs ļauj izteikt pieņēmumu, ka vērtētas tika tikai pareizās atbildes, turklāt vienīgajā, skolotājas iedomātajā, pieraksta veidā. Protams, matemātikā ir situācijas, kurās ir atbilstoši vērtēt tikai atbildes (pareizi/nepareizi), bet ne šajā un arī ne vairumā gadījumā.
Saņemot novērtējumu 0 punkti (no 5 iespējamiem), skolēns (un vecāki) iegūst informāciju – par to, kas ir skaitļa “kaimiņi”, tu nezini pilnīgi neko. Vai skolēna sniegums tam atbilst?
Šāda situācija neveidotos, ja vērtēšanā izmantotu snieguma līmeņu aprakstus, piemēram, kādi risinājumi liecina, ka 1) sāk tikai saprast un visos gadījumos uzrakstīt “kaimiņus” vēl nevar, 2) ir sapratis, kas ir skaitļa “kaimiņi”, bet vēl pieļauj 1–2 kļūdas, 3) saprot, kas ir skaitļu „kaimiņi” un nekļūdās, tos pierakstot.
Pareizas var būt arī dažādas atbildes
Nav korekti šajā situācijā vainot tikai konkrēto skolotāju. Piemēram, ir pamats pieņēmumam, ka arī izmantotā mācību līdzekļa autori te redz iespēju vērtēt tikai atbildes pareizību (cik skaitļu trijnieku, tik punktu). Arī kopumā šāda pieeja skolēna darbības novērtēšanā tikai atspoguļo mūsu kolektīvo pieredzi, prioritātes un metodiskos uzstādījumus matemātikas mācīšanā līdz šim – tradīcijā primārais (īpaši skumji, ka tas tipiski raksturo sākumskolu) ir vienīgais pareizais atrisinājuma veids un/vai tā pieraksta veids.
Dažādu (pareizu!) atrisinājumu akceptēšana ir viens no aspektiem, kam jāpievērš uzmanība jaunā saturā ieviešanā. Ilustrācijai vēl viens piemērs, kas to uzskatāmi parāda.
Skolēnam jārisina uzdevums:

Skolotāja labojums skolēna atbildei:

Skolēni domā dažādi
Skaidru vērtēšanas mērķu izvirzīšana un kritēriju formulēšana, kā arī dažādu atrisinājumu un to pieraksta veidu akceptēšana faktiski ir sekundāri jautājumi; primāri ir pieņemt atziņu, ka skolēni domā dažādi, ka katra skolēna matemātiskās darbības pieredzei (jo īpaši sākumskolā!) jābalstās tajā, kā viņš domā, kādas ir viņa stratēģijas. Skolotāja uzdevums ir šo procesu atbalstīt, vadīt, precizēt un, ja nepieciešams, arī labot.
Skaties vairāk:
Kā mainīsies mācīšanas pieeja matemātikā?", Jānis Vilciņš, Skola2030
http://bit.ly/pieejamatematika
Uzsvari matemātikā, Jānis Vilciņš, Skola2030
http://bit.ly/matematika_uzsvari
Diskusija Twitter telpā:
https://twitter.com/gaismonis/status/1205558965049933825?s=20